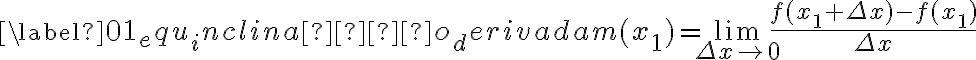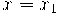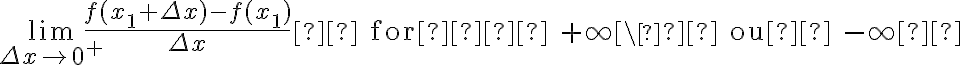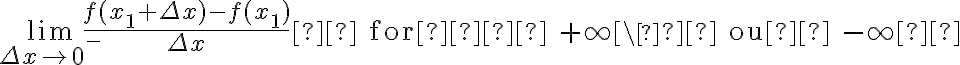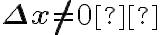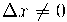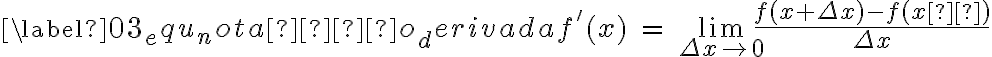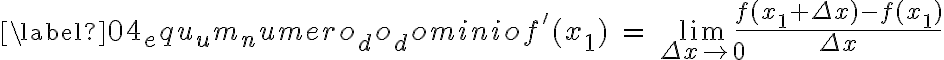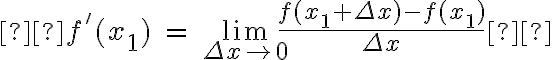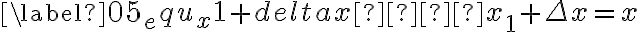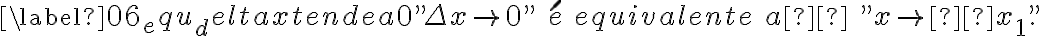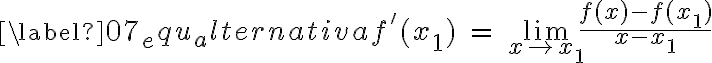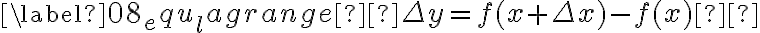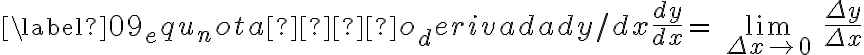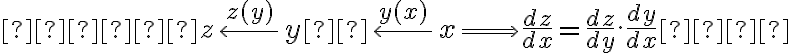Definição Derivadas
Definição Derivadas
Definição Derivadas
Segundo Leithold (1994, p. 139) "a reta tangente ao gráfico de uma função em um dos seus pontos, começamos pensando em definir a inclinação da reta tangente no ponto. Então a tangente é determinada por sua inclinação e pelo ponto de tangência".
Assim, a reta tangente ao gráfico em uma função contínua, é definida conforme descrito abaixo:
1. Definição. Suponhamos que a função 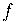 seja contínua em
seja contínua em 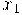 . A
. A 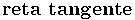 ao gráfico de
ao gráfico de 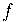 no ponto
no ponto 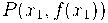 é
é
(i) a reta por 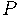 tendo inclinação
tendo inclinação 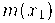 , dada por
, dada por
se o limite existir;
e
Se nem (i) nem (ii) da Definição1 forem verdadeiras, então não existirá reta tangente ao gráfico de 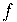 , no ponto
, no ponto 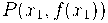 . (LEITHOLD, 1994, p. 140)
. (LEITHOLD, 1994, p. 140)
A variação dos valores de 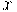 ou incremento de
ou incremento de 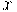 , é denotado pela diferença entre abscissas, como
, é denotado pela diferença entre abscissas, como 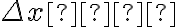 , (lemos "delta x").
, (lemos "delta x").
Leithold (1994 ) no caso de 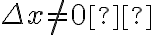 , e o limite existir, podemos dividir o numerador e o denominador por
, e o limite existir, podemos dividir o numerador e o denominador por  , para calcular o valor da inclinação de
, para calcular o valor da inclinação de 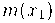 .
.
Leithold (1994) Uma reta horizontal não tem inclinação, pois, é paralela ao eixo das abscissas.
Segundo Leithold (1994, p. 142) " A 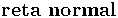 a um gráfico em um dado ponto é a reta perpendicular à reta tangente naquele ponto". Ressalta a importância que existe para o Cálculo na utilização do tipo de limite, para encontrar a inclinação da reta tangente descrito na Definição 1, então apresenta a notação de derivada:
a um gráfico em um dado ponto é a reta perpendicular à reta tangente naquele ponto". Ressalta a importância que existe para o Cálculo na utilização do tipo de limite, para encontrar a inclinação da reta tangente descrito na Definição 1, então apresenta a notação de derivada:
2. Definição. A 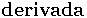 de uma função
de uma função 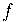 é a função denotada por
é a função denotada por 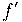 , tal que seu valor em qualquer número
, tal que seu valor em qualquer número 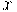 do domínio da
do domínio da 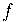 seja dado por
seja dado por
se esse limite existir. (LEITHOLD, 1994, p. 142)
Leithold (1994) Se 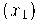 for um determinado número do domínio de
for um determinado número do domínio de 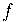 , então
, então
Quando existir o limite. Fazendo a comparação das fórmulas (1). e (4). como referência, percebemos que a inclinação da reta tangente a 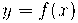 no ponto
no ponto 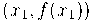 é exatamente a derivada de
é exatamente a derivada de 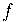 calculada em
calculada em 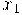 .
.
Vamos considerar agora a fórmula (4) que é
Nessa fórmula seja
Então
Das fórmulas , (4),(5) e (6) obtemos a seguinte fórmula para 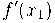 :
:
se o limite existir. A fórmula (7) é uma alternativa para (4) no cálculo de 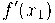 .
.
Leithold (1994) A notação de derivada 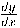 introduzida Gottfried Wilhelm Leibniz, porém, em trabalhos independentes Leibniz e Sir Isaac Newton introduziram quase ao mesmo tempo, o conceito de derivada. Então são exibidas estas notações para derivada:
introduzida Gottfried Wilhelm Leibniz, porém, em trabalhos independentes Leibniz e Sir Isaac Newton introduziram quase ao mesmo tempo, o conceito de derivada. Então são exibidas estas notações para derivada:
O uso do símbolo 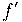 para a derivada da função
para a derivada da função 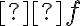 , foi introduzida pelo matemático francês Joseph Louis Lagrange (1736-1813), no século dezoito. Essa notação indica que a
, foi introduzida pelo matemático francês Joseph Louis Lagrange (1736-1813), no século dezoito. Essa notação indica que a 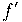 é derivada da função
é derivada da função 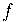 e seu valor em
e seu valor em 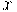 é
é 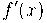 .
.
Se 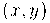 for um ponto do gráfico de
for um ponto do gráfico de 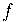 , então
, então 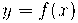 e
e 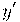 também será usado como notação para a derivada de
também será usado como notação para a derivada de 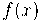 . Com a função
. Com a função 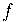 definida pela equação
definida pela equação 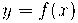 , podemos expressar
, podemos expressar
onde 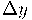 é chamado de incremento de
é chamado de incremento de 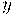 e denota a variação no valor da função quando
e denota a variação no valor da função quando 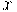 varia de
varia de 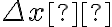 . Usando (8) e escrevendo
. Usando (8) e escrevendo 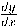 em lugar de
em lugar de 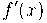 a fórmula (3) torna-se
a fórmula (3) torna-se
Em relação ao estudo das derivadas em nosso trabalho, não podemos deixar de fazer referência a esta importante ferramenta matemática, denominada regra da cadeia. O recurso da regra da cadeia, essencial na derivação de funções compostas, além, da dedução das funções trigonométricas.
Segundo Rezende (2003, p. 351) "[...] A interpretação da regra da cadeia, pensando em derivada como taxa de variação instantânea, e usando a notação de Leibniz, torna o significado dessa regra muito mais transparente:"
Recurso matemático importantíssimo, definida pelo Teorema da regra da cadeia segundo Leithold (1994, p. 183) "Se a função 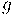 for derivável em
for derivável em 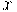 e a função
e a função 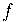 for derivável em
for derivável em 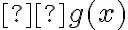 , então a função composta
, então a função composta 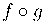 será derivável em
será derivável em 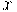 , e
, e 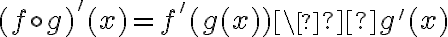 ."
."
Enfatizando que nosso propósito é apresentar os conceitos e definições pertinentes ao curso de Cálculo, como a diferenciação (diferenças infinitamente pequenas).
Segundo Rezende (2003, p. 84) "A história do Cálculo é longa demais para ser abreviada, e fecunda o suficiente para se fazer recortes superficiais, mas, mesmo assim, tentaremos fazer um “breve” relato da evolução histórica [...]".
Acreditamos ter alcançado o objetivo, em mencionarmos alguns aspectos, primordiais para uma maior compreensão da essência deste material, pois, não é o propósito deste trabalho aprofundar-se nestes temas.